Friday, April 27, 2012

CMA1390—-THE BEST ACRYLIC SOLUTION « handbag

You are still in the trouble that how to cut acrylic? You are still thinking how to handle acrylic incision with bubbles and how to edge? Hans YueMing laser has been committed to cutting scheme study and solution more than 30 years. The appearance of CMA1390, make all the cutting problem be smoothly done or easily solved.

Hans YueMing laser CMA1390 laser cutting machine has the following advantages:

1. The imported 4 balanced linear guide, work stability, high accuracy

2. Speed reducing driving makes the machine longer working life

3 USB interface, large capacity memory, can process multiple files, download data conveniently, quickly, output data can be layered on each floor can be defined separately, the output power, output speed, laser mode ( engraving, cutting), and each layer is defined parameters automatically save.

4 The coaxial red positioning system, precise optical path adjustment, convenient, quick.

5. The dichroic output management.

6 .Selection of high-quality laser, beam quality, long service life

7. Imported focusing mirror, thinner spot, stronger cutting force.

8 The carving process for attenuation compensation, to ensure that different regions of the carving effect are the same

9. The shortest path optimization function, greatly improve the work efficiency

10. Perfect dust proof design, greatly improves the performance of whole stability

11. Good compatibility, can support PLT, BMP, DSB, DST, DXF and other formats

12. With ROHS and CE certification

After 20 years of market test of wind and rain, the global synchronization of sales prove that Hans YueMing laser cutting machine with fully computerized operation, humanized design, the optimal cost-effective and peer reputation, fill the engraving machine cannot be cut, cutting machine cannot carving industry blank. Marvelous carving, incomparable cutting (high precision half cut / cutting process), 1524mm / s high speed, ultra accelerated long-term trouble-free operation, is the current laser cutting machine in Supreme choice.

This entry was posted and is filed under handbag. Both comments and pings are currently closed.

Posted by Houoop at 8:22 PM 1 comments

Cutting a Graph By the Numbers « Gödel's Lost Letter and P=NP


Old algebra helps build new algorithms

Nisheeth Vishnoi is a theorist at Microsoft Research who has many pretty results. Some of them require great technical expertise—the main idea may be clear, but the execution is quite difficult. Others of his results require less technical expertise, but their proofs depend on a flash of deep insight. It is rare, in my experience, to find this combination in one person.

Today I would like to talk about his recent talk at GIT on finding a balanced separator in an undirected graph. It was a beautiful talk that explained a proof of the former kind: clear ideas but very technical details.

This work is joint with Lorenzo Orecchia and Sushant Sachdeva and will appear in the next STOC—the paper is entitled “Approximating the Exponential, the Lanczos Method and an 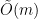{\tilde{O}(m)}-Time Spectral Algorithm for Balanced Separator.”

One thing I really appreciate is that although the algorithm works on graphs and gives you a graph decomposition, the key ingredients are numerical and algebraic. A 37-year old result on polynomial approximations is combined with matrix algebra. As soon as you hear “matrix” you might think that algorithms of time 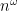{n^\omega} are involved, where 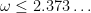{\omega \leq 2.373\dots} is the exponent of matrix multiplication, but no, the time stays strictly less even when the 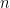{n}-vertex graphs have 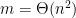{m = \Theta(n^2)} edges.

Advisee Disclaimer

Before I start discussing this work (OSV) I must disclose that I was once Nisheeth’s Ph.D. advisor—perhaps you are always your students’ Ph.D. advisor, even after they graduate. But I do not really know where he got the tremendous ability that he demonstrates now, since I cannot imagine that it came from my advising. He was great as a student, great as a colleague when at Tech, yet now he seems to operate at a higher level. Ah, well.

This phenomenon of students being better than their advisors has happened to me many times. It reminds me of a question that Ken Steiglitz used to ask me years ago. He wanted to know how we could make objects to extremely small tolerances when as humans we could only see fairly large differences? Another way to ask this is:

With tools that operate only to within a tolerance of 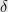{\delta} how can we make objects that have tolerances of {\epsilon}, where { \epsilon \ll \delta}?

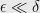Let’s leave that discussion for another day and move on to the result of OSV.

Cutting Graphs

Undirected graphs ares used to model countless things in computer science; if they did not already exist, we would have had to invent them. Hence finding algorithms that decompose graphs efficiently is extremely important to theory in general, and to creating graph algorithms in particular. Decompositions can be used to create recursive algorithms and to solve many other problems on graphs.

One of the reasons that binary trees are often an accessible class of graphs is that they satisfy the following beautiful result:

Theorem: Let 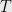{T} be a binary tree on 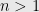{n>1} vertices. Then there is an edge {e} whose removal cuts the tree 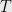{T} into two pieces, and each is of size at least 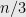{n/3}. Moreover the edge {e} can be found in linear time.


(source, S’09 final)

There are three features to this theorem that make it useful:

  1. The cut is small: it consists of a single edge.
  2. The two pieces are balanced: each is at least half the size of the other.
  3. The cut can be found in linear time.

I would love to report that this theorem on binary trees generalized to all graphs, or even to all bounded degree graphs. Of course this is false. There are bounded-degree graphs such that all balanced cuts have size 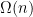{\Omega(n)}. This follows even if we weaken the notion of balanced to allow a piece to be only a 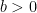{b>0} fraction of the other, and even if we do not require that there is a polynomial time algorithm to find the cut.

There is a property called conductance of a graph, usually denoted by 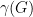{\gamma(G)}, that measures how well the graph can be cut into two pieces. The main result of OSV is a new theorem that settles the question of designing asymptotically optimal algorithms for finding balanced cuts.

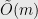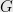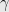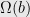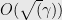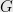Theorem: There is a {\tilde{O}(m)}-time algorithm that given an undirected graph {G}, a constant balance {b \in (0,1/2]}, and a parameter {\gamma}, either finds an {\Omega(b)}-balanced cut of conductance {O(\sqrt(\gamma))} in {G}, or outputs a certificate that all 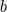{b}-balanced cuts in 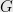{G} have conductance at least {\gamma}.

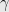The theorem is about as good as one can expect. The cut is balanced and its size is controlled by the conductance as it must be. Also the algorithm runs in 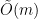{\tilde{O}(m)} time.

Almost Linear

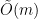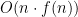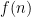In this paper and elsewhere you will see the phrase “almost linear,” and it is denoted by adding a tilde to the “O:” as in {\tilde{O}(m)}. This means that the algorithm in question runs in time {O(n\cdot f(n))} where {f(n)} is a product of terms that depend only logarithmically on 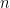{n} and all other parameters. We would prefer a truly linear time algorithm, but given the state of our understanding, often almost linear is the best we can do. So we do what we can.

An Old Theorem

OSV’s paper depends on a rather surprising result by Edward Saff, Arnold Schönhage, and Richard Varga (SSV), which proves the existence of a very good rational approximation to the function 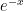{e^{-x}} on the entire interval 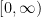{[0,\infty)}. As given in Corollary 6.9 on page 35 of OSV, SSV proved in 1975:

Theorem: For any integer 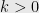{k>0}, there exists a degree 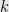{k} polynomial 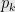{p_{k}} such that 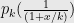{p_{k}( \frac{1}{(1+x/k)})} approximates 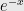{e^{-x}} up to an error of 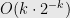{O(k\cdot 2^{-k})} over the interval {[0,\infty)}.

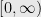Note, the theorem proves only the existence of this good approximation, and this is one of the issues that OSV must overcome.

The reason that having a good rational approximation is important is that OSV uses this on matrices: this allows a certain linear algebra problem to be solved very fast. We will now turn and discuss this theorem.

A New Theorem

In order to prove their theorem, OSV must be able to compute an exponential of a matrix fast. They do this by using SSV and quite a number of other tricks. The main result is:

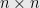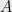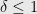Theorem: Given an {n \times n} SDD matrix {A}, a vector {v}, and a parameter {\delta \le 1}, we can compute a vector {u} such that

\displaystyle || \exp(-A)v - u|| \le \delta ||u||.

Further the algorithm runs in time 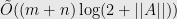{\tilde{O}((m + n)\log(2 +||A||))}.

Here SDD means that the matrix is symmetric and diagonally dominant. They use the beautiful work of Daniel Spielman and Shang-Hua Teng on approximately inverting matrices. One of the very technical details is the error analysis, since the approximation to the inverses they get from Spielman-Teng interact in a complex way with the error bounds of SSV. As usual read the paper for details.

Open Problems

Can the result of SSV be used elsewhere? Are all linear algebra problems almost linear?

[fixed OSV theorem statement, fixed vertex v --> edge e in tree lemma statement, and sourced lemma]

Posted by Houoop at 7:07 PM 0 comments